「なんだかウチの会社、
納期遅れが多い気がするんだよなー。。」
このあいまいな不安を、DMAICを使って徹底的に数値化して
具体的な対策方法に落とし込みます。
DMAIC 3番目のプロセス「A」を、具体的に解説していきましょう。

前項「M」の数値化プロセスで、
問題解決に関連する因子を抽出し、それを数値化してきました。
これはあいまいな因子をロジカルに解決するために、非常に重要なプロセスです。
そして、もうひとつ重要な点は
「D」「M」で列挙した因子たちは、
問題解決するかもしれない
その程度の正確さ しか持っていない。
ということです。
列挙した因子たちを、すべて実行しようとすると
いくら時間とリソースがあっても足りません。
そして結局、解決に至らず
「ウチの会社は結局ムリなんだ。。」
となってしまいます。
本当に解決するには、
問題の原因がどこにあるのか
これを分析しないといけません。
それが本項「A」の分析プロセスになります。
分析といっても、エクセルで数回ポチポチするだけでできる方法を紹介しますので
是非、実際の現場で試してみてください。
ここでは、様々な現場で応用がきく
「回帰分析」について解説していきます。
聞きなれないかもしれませんが、
「思いついた解決策Aは、本当に問題解決につながるのか?」
が分かる最強のプロセスです。
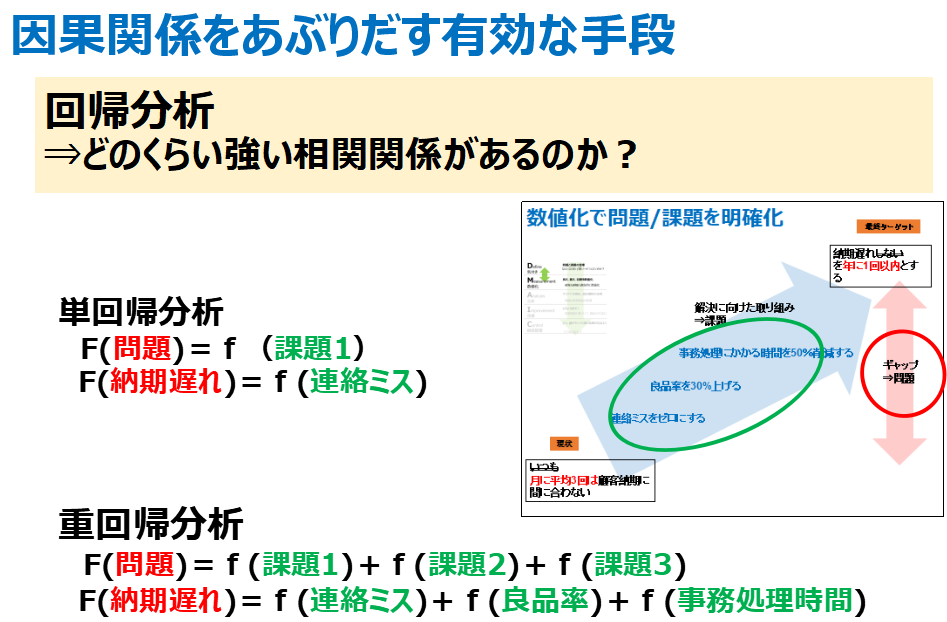
問題に関わる因子(課題)が一つの場合・・・
例えば、「納期遅れする」問題に対して、「連絡ミス」にのみを解決策とする場合
単回帰分析をします。
問題に関わる因子(課題)が複数の場合
例えば、「納期遅れする」問題に対して、「連絡ミス」、「良品率」、「事務処理時間」を
解決策とする場合は、重回帰分析をします。
それぞれ詳しく見ていきましょう。

単回帰分析という難しい名前がついてますが、エクセルで散布図を描くだけです。
原因を横軸、結果を縦軸にグラフ化して傾向を把握する手法ですね。
別投稿でも解説しているので参考にして下さい
上図のように、納期遅れ回数(問題)と連絡ミス回数(課題)をエクセルに入力し、
4回ポチポチするだけで、単回帰分析できるグラフ(散布図)が出来上がります。
では出来上がった散布図を見ていきましょう。
点の分布だけでは、なんとなく右上がり?、右下がり?、バラバラ?
程度の定性的な情報しか得られません。
しかし、ここからがポイント
近似式を描いて、決定係数を表示しましょう。
(グラフ中のデータポイントを右クリックするとすぐに表示できます)
近似式は、
得られたデータポイントを関数式で近似してくれる便利な機能です。
一次関数、多項式、対数・・などなど、
ポチポチするだけでいろんなグラフをフィッティングしてくれます。
そして、決定係数R^2
この値は、どれだけ近似式が確からしいか を示しています。
この値が大きいほど、データと近似式は等しい と言うことができ
少なくとも0.85より大きい場合には、確からしいと言えます。
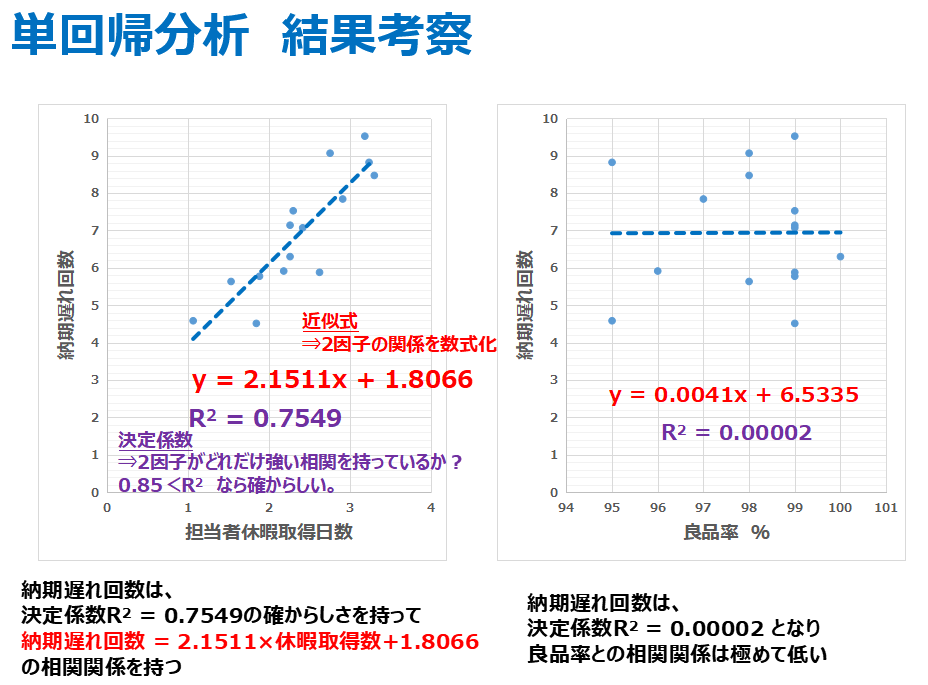
上のグラフを見てみましょう
左のグラフは、納期遅れ回数 vs 担当者休暇取得日数 を表した単回帰式です。
近似式 : Y(納期遅れ回数)=2.1511×(担当者休暇取得日数)+1.8066
の一次関数で示すことができ、
その決定係数は0.7549 となり、まぁまぁ確からしいと言えます。
一方で右のグラフは、納期遅れ回数 vs 良品率 を表した単回帰式です。
見るからにバラバラで関係なさそうですね。
無理やり近似式を描くと
Y(納期遅れ回数)=0.0041×(担当者休暇取得日数)+6.5335
の一次関数で示すことができ、
その決定係数は0.00002 となり、極めて関係性は薄い言えます。
これらの結果から、「D」や「M」で列挙してきた課題(問題を解決する因子)の中から
問題(納期遅れ)に関係の強い因子のみを抽出するのです。
これで大きく工数、リソースを削減することができます。
次に、複数の因子が関連する場合を考えてみましょう。
我々が直面する問題は、複数の因子が関連していることが多いです。
そんな時に活躍してくれるのが、重回帰分析です。
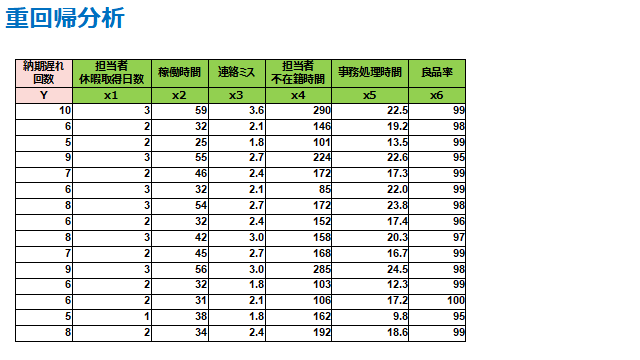
例えば、上記のように
納期遅れ(問題)に関わる因子として
担当者休暇取得日数、担当者の移動時間、連絡ミス回数、担当者不在時間、事務処理時間、良品率
を列挙したとしましょう。
どの因子が重要か分からないと、すべて対策することになりリソースが足りません。
そこで、同様にエクセルを活用して重回帰分析をして
どの因子が、どのような関係式で、どのくらい強く 関連しているか
調べていきます。
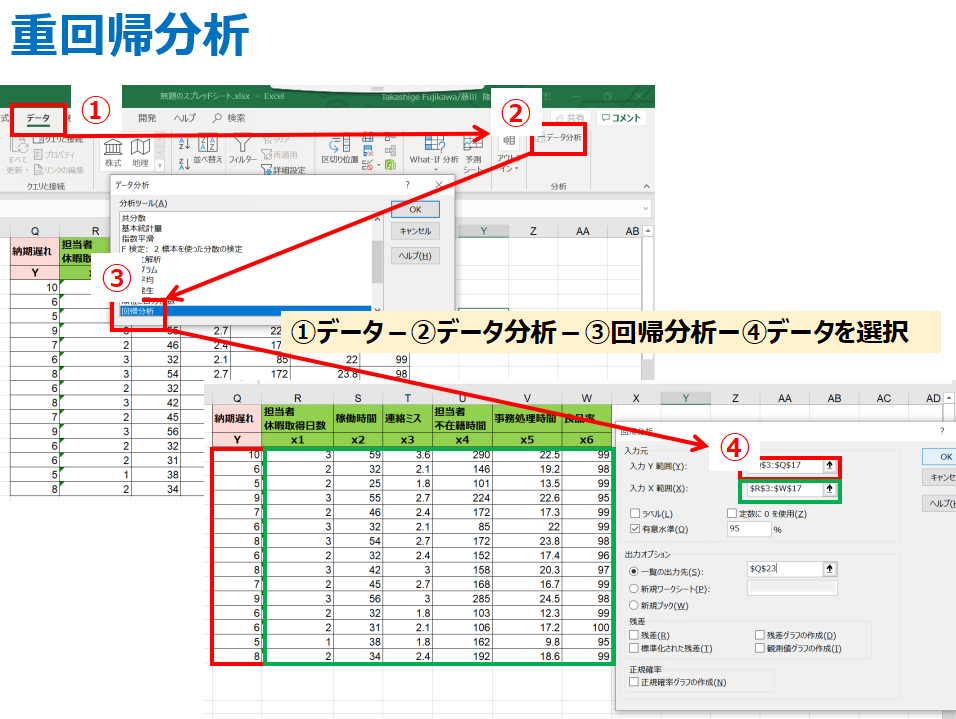
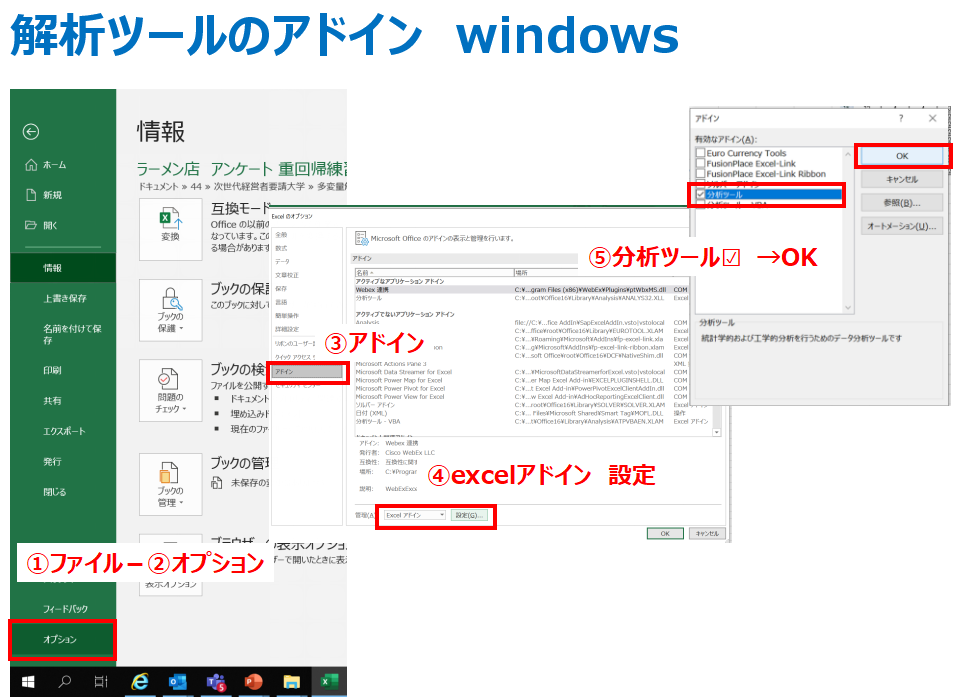
エクセルの分析ツールを活用して
上記のように4回ポチポチすると、エクセルが計算してくれます。
本当に便利ですね。
分析ツールの設定方法はこちらを参考にしてください。

そして、得られた重回帰分析結果がこちらになります。
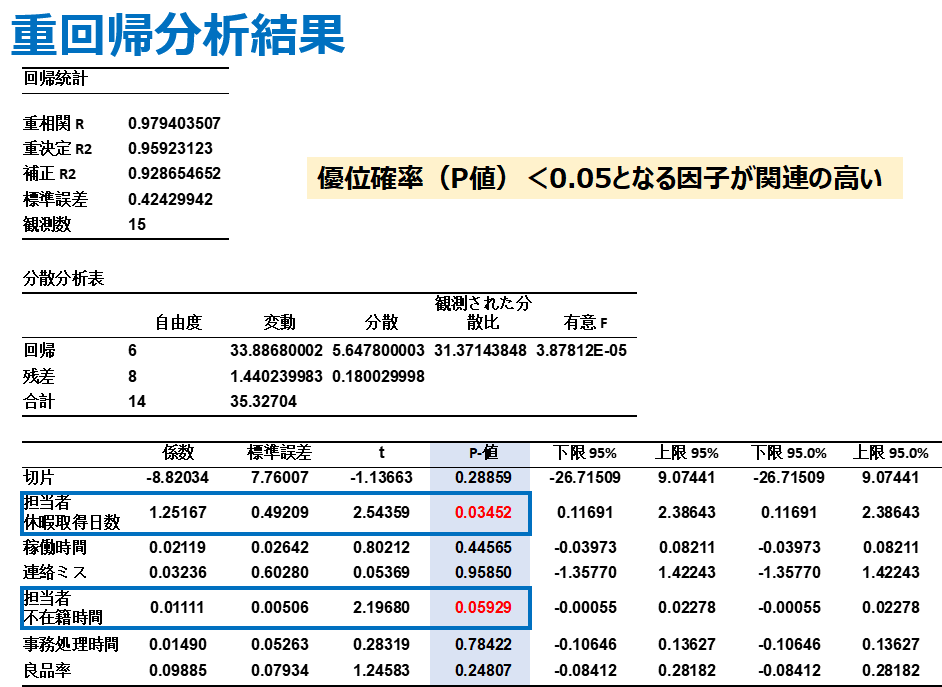
たくさん数字が出てきますが、まずはP値に注目してください。
P値は「provability」の略で、確からしさを示す「優位確立」です。
P値が0.05よりも小さい因子は、問題に対して関連が強いと言えます。
逆に言えば、その他の移動時間、連絡ミス回数、事務処理時間、良品率は
納期遅れには全く関係ない ということが言えます。
これらの対策を実施する工数をバッサリ切り捨てられるので、お得ですね。
ここでは、担当者休暇取得日数と担当者不在時間が関連が強い、と分析できましたね。
次に、関係ないと分かった邪魔な因子を省いて、
この2つの因子だけを使って、もう一度多変量解析します。
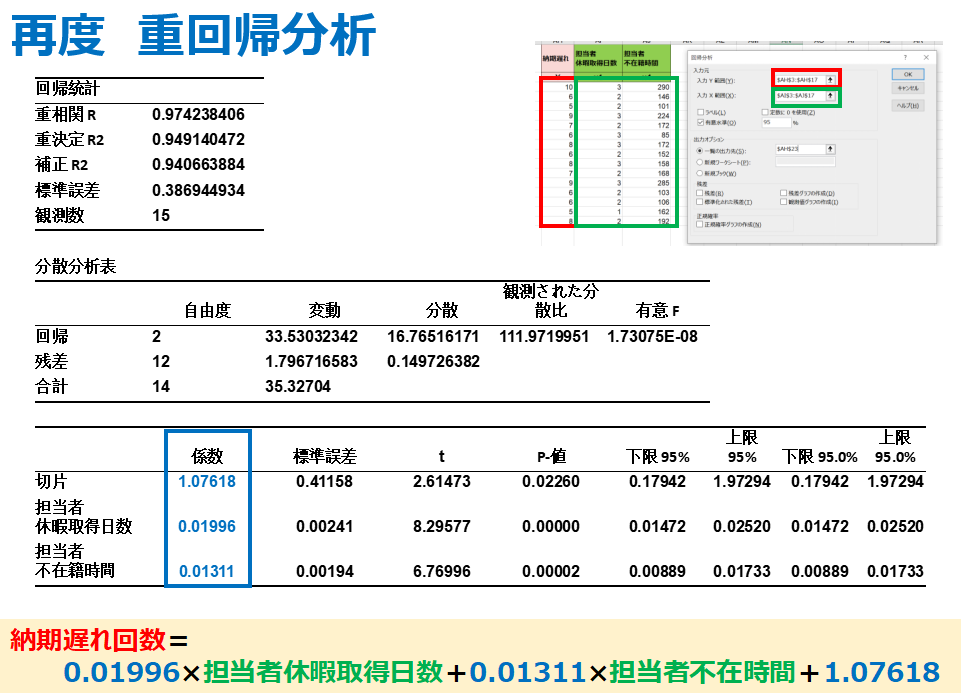
すると、それぞれの因子に関わる係数が得られます。
この係数を活用して得られる重回帰式は
納期遅れ回数=
0.01996×担当者休暇取得日数+0.01311×担当者不在時間+1.07618
となり、納期遅れ回数が、担当者休暇日数と不在時間の関数で表すことができます。

まとめていきましょう。
DMAIC 3番目のプロセス「A」分析は、
問題と課題因子がどれだけ関係あるか?
を分析していくプロセスです。
ひとつの例として、回帰分析を紹介しました。
関係のない因子を切り捨て、効果の高い因子に集中する
そうすることで、少ない工数で高い効果を出すことができますね。
では次に、4番目のプロセス「I」improveで改善を進めていきましょう。


コメント