みなさんこんにちは。
今日は、聞いたことはあるけど、何者なのかよくわからない
特殊相対性理論に迫りたいと思います。
ちなみに私も専門外ですが
小学校で習う「時間・速さ・距離」の関係 と 中学校で習う三平方の定理

で理解できる感動を皆様にも感じていただけたらと思います。
今回は、ご存じアインシュタインが提唱した特殊相対性理論の中の
「時間の遅れ」についてお話していきます。
浦島太郎のように、戻ってみたら周りがみんな年を取っていた・・
とまではいきませんが、
宇宙を遊泳しているスペースシャトル内の時計は進むのが遅い
という現象が実際に観測されています。
つまり、動いているものは時間の流れが遅い、ということです。
この現象がどういう理屈で成り立っているのか、速さ・時間・距離の関係式と三平方の定理を使って証明していきます。
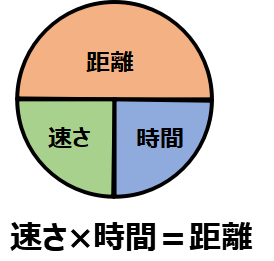
では、まずそれぞれの復習から行きましょう。
速さ・時間・距離の関係は小学校で習いましたね。
速さ × 時間 = 距離
「速度v1で登校したA君に、速度v2で追いかけて
忘れ物を届けるお母さんは何分後に追いつくでしょう?」
といった、ややわざとらしい演出のアレです(笑)

三平方の定理はピタゴラスによって示された直角三角形の
各辺の長さに関わる関係式
a^2+b^2=C^2
美しいですね。
そして、いよいよ本題に入っていきます。
簡単な状況を設定して考えていきましょう。
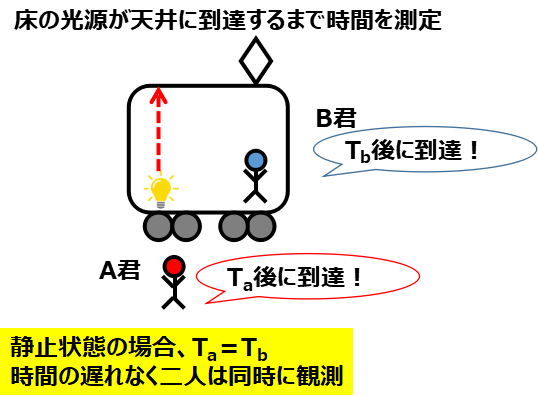
まず、止まっている電車の中に光源があり、外にいるA君と中にいるB君がその光が天井に到達するまでの時間を測定している
という状況を想定しましょう。
光の速さをCとし、Ta後に観測した場合
速さ・時間・距離の関係式から
光源から天井までの距離 = C×Ta
と言えますね。
そして、静止している系では時間の遅れは無いので
Ta=Tb となりA君もB君も同時に到達したと観測します。
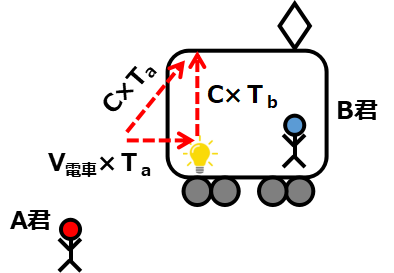
次に電車を動かしてみましょう。
同じく電車の中にある光源がV電車の速度で動いた場合、A君とB君には
光がどのように見えるでしょうか?
B君は光源と一緒に動いているので、状況は変わらずTb後に光の到達を観測します。
しかし今回A君が観測した時間Taは電車が動いた距離も考慮する必要があります。
速さ・時間・距離の関係式から、それぞれの距離を算出すると
B君が観測した光源~天井までの距離 = C×Tb
A君が観測した光源~天井までの距離 = C×Ta
電車が動いた距離 = V電車×Ta
と言えますね。
ここで三平方の定理の登場です。
それぞれの距離(=辺の長さ)を代入すると
(C×Ta)2 =(V電車×Ta)2 +(C×Tb)2
両辺をCで割って
Ta2 =(V電車/C)2×Ta2 +Tb2
移項すると
Tb2 =(1-(V電車/C)2)×Ta2
両辺の平方根を取ると
Tb =(1-(V電車/C)2)1/2×Ta
となります。
ここで、光速Cは 299,792,458 m/s と、めちゃくちゃ速いので
(V電車/C)<1となり、
(1-(V電車/C)2)1/2<1となります。
つまり、Tb<Taとなり
静止しているA君の時間が早く流れる、ということになります。
光の速さは不変、という原理原則から距離が変化した辻褄を時間で合わせるしかない
という理屈ですね。


コメント